Datos nominales frente a datos ordinales: comprensión de las diferencias clave

En esta sección, los lectores aprenderán qué distingue a los datos nominales de los ordinales, por qué estas categorías son importantes en la ciencia de datos moderna y cómo comprender su función mejora la precisión del análisis de datos y la interpretación estadística. Descubrirán cómo influye cada tipo de dato en las escalas de medición, verán ejemplos reales de variables nominales y ordinales, y comprenderán su relevancia en la investigación de datos cuantitativos y cualitativos.
Antes de adentrarnos en las definiciones, conviene explicar por qué este tema es importante. En una era donde las empresas procesan billones de datos a diario, la forma en que clasificamos los datos influye directamente en nuestra capacidad para tomar decisiones acertadas. Esta sección presenta las diferencias fundamentales entre datos nominales y datos ordinales, ambos cruciales para el razonamiento estadístico y la obtención de información a partir de los datos.
Comprensión de los tipos de datos
Todos los datos comienzan como información no estructurada. Una vez organizados mediante la recopilación de datos, se convierten en la base de la ciencia de datos moderna. Los datos existen en numerosas formas —binarias (0 y 1), texto, imágenes o audio— y pueden analizarse mediante técnicas de datos tanto cualitativas como cuantitativas. Reconocer el tipo de datos ayuda a determinar la escala de medición y los métodos estadísticos adecuados.
Cada vez más analistas destacan que conocer el tipo de datos es tan crucial como los datos mismos. Según una encuesta de PwC de 2025, el 84 % de los profesionales de datos afirmó que etiquetar incorrectamente los tipos de datos genera resultados analíticos erróneos, lo que refuerza la necesidad de prácticas adecuadas de medición de datos.
Datos categóricos y cuantitativos
Los datos generalmente se dividen en dos categorías principales: categóricos y cuantitativos.
- Los datos categóricos (o datos cualitativos) describen características como el color, el género o la preferencia de marca. Incluyen datos nominales y datos ordinales.
- Los datos cuantitativos (o datos numéricos) implican valores medibles e incluyen tipos de datos de intervalo, de razón, discretos y continuos.
Comprender la diferencia entre datos nominales, ordinales, de intervalo y de razón es clave para realizar análisis estadísticos correctos y extraer conclusiones válidas.
Niveles de medición: nominal, ordinal, de intervalo y de razón.
El psicólogo Stanley Smith Stevens definió los cuatro niveles de medición que todavía se utilizan hoy en día:
- Escala nominal (datos nominales): Categoriza sin implicar orden. Ejemplos de datos nominales incluyen género, grupo sanguíneo y país.
- Escala ordinal (datos ordinales): Ordena las categorías de manera significativa, como el nivel educativo o los niveles de satisfacción, aunque los intervalos entre rangos pueden variar.
- Escala de intervalo (datos de intervalo): Se ocupa de variables numéricas medidas a lo largo de intervalos iguales pero sin un cero verdadero (por ejemplo, la temperatura en grados Celsius).
- Escala de razón (datos de razón): Presenta un cero absoluto, lo que permite realizar operaciones matemáticas completas. Algunos ejemplos son la altura, los ingresos y la duración.
Cada escala de medición ofrece una perspectiva única para comprender los datos. Los datos nominales y ordinales pertenecen a la categoría de datos categóricos, mientras que los datos de intervalo y de razón se clasifican como datos cuantitativos.
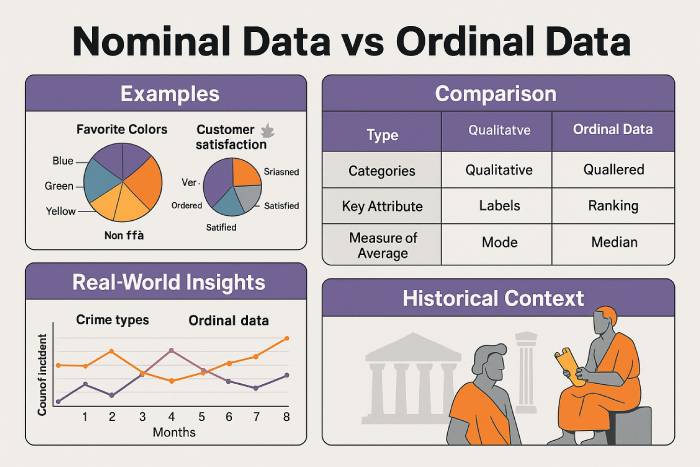
Explicación de los datos nominales
Los datos nominales son un tipo de datos cualitativos que se utilizan para clasificar la información sin orden ni jerarquía. Este nivel nominal es común en marketing, investigación y atención médica.
Ejemplos de datos nominales:
- Género (masculino, femenino, otro)
- Grupo sanguíneo (A, B, AB, O)
- Color de ojos (azul, marrón, verde)
- Segmentos de clientes (nuevos, recurrentes, premium)
En el análisis de datos, las variables nominales se examinan mediante la moda y la frecuencia. Los gráficos de barras y los gráficos circulares representan eficazmente estos datos categóricos, lo que ayuda a visualizar proporciones y tendencias.
Datos ordinales y su importancia
Los datos ordinales representan categorías ordenadas —como índices de satisfacción o clasificaciones de desempeño— donde las distancias entre los valores no son iguales. Esta escala ordinal se utiliza a menudo en técnicas de recopilación de datos como las encuestas.
Ejemplos de datos ordinales:
- Nivel educativo (bachillerato, licenciatura, máster, doctorado)
- Niveles de satisfacción (muy insatisfecho → muy satisfecho)
- Clase económica (baja → media → alta)
En el análisis de datos, los datos ordinales permiten el uso de medianas, percentiles y pruebas no paramétricas. Visualizaciones como los gráficos de barras ordenadas y los diagramas de puntos muestran claramente las relaciones de orden. La principal diferencia entre los datos nominales y ordinales radica en el orden: los datos ordinales lo poseen, mientras que los nominales no.
Datos de intervalo y de razón: Análisis cuantitativo
Los datos de intervalo y de razón son los tipos de datos cuantitativos más precisos.
- Los datos de intervalo utilizan una escala de intervalo con intervalos de medición iguales pero sin cero absoluto (por ejemplo, CI, temperatura).
- Los datos de razón operan en una escala de razón, donde cero significa la ausencia total de una variable. Algunos ejemplos son los ingresos, el peso o la distancia.
Ambos tipos de datos permiten realizar análisis estadísticos avanzados, como la media, la varianza y la correlación, esenciales en la estadística descriptiva y la modelización predictiva.
Datos discretos frente a datos continuos
Los datos cuantitativos también se dividen en datos discretos y continuos:
- Los datos discretos incluyen valores contables como el número de clientes o coches en un lote.
- Los datos continuos implican valores medibles dentro de un rango, como la altura o el tiempo.
Reconocer las distinciones entre datos discretos y ordinales, y entre datos discretos y continuos, mejora la precisión del análisis de datos y garantiza que se utilicen los métodos de visualización adecuados.
Por qué es importante comprender los tipos y niveles de datos
La correcta identificación de datos nominales, ordinales, de intervalo y de razón influye directamente en la fiabilidad de los análisis estadísticos. Tratar los datos ordinales como puramente numéricos o nominales puede generar interpretaciones sesgadas. Como señala la Dra. Lisa Nguyen de la Universidad de California, «la mala interpretación del tipo de datos es una de las causas silenciosas de sesgo en los modelos de aprendizaje automático».
Un estudio de Deloitte de 2025 reveló que el 71 % de las empresas que invirtieron en iniciativas de ciencia de datos reportaron mejoras cuantificables en el retorno de la inversión tras capacitar a su personal en clasificación de datos y manejo de escalas de medición. Esto pone de manifiesto la creciente demanda de analistas con experiencia en la recopilación, categorización e interpretación de datos.
Opiniones de expertos y perspectivas para 2025
Según IDC (2025), la generación global de datos superó los 181 zettabytes, un aumento del 23% con respecto a 2024. La Dra. Maria Chen del MIT afirma: “Reconocer los matices entre los datos nominales y los datos ordinales va más allá del ámbito académico; es fundamental para el análisis aplicado”.
El Dr. Rafael Torres, del Instituto Europeo de Ciencia de Datos, añade: “El futuro reside en el modelado de datos híbrido: combinar datos cualitativos y cuantitativos para obtener una comprensión más profunda del comportamiento”.
Un informe de Statista (2025) reveló que el 78 % de las organizaciones utilizan la toma de decisiones basada en datos, pero casi la mitad se enfrenta a problemas de clasificación errónea. Esto demuestra por qué dominar distinciones como datos nominales frente a ordinales, datos de intervalo y de razón, y datos discretos frente a continuos sigue siendo fundamental para los analistas modernos.
Tablas visuales y estudios de casos reales
| Tipo de datos | Escala | Propiedad de medición | Ejemplo | Utilizado en |
|---|---|---|---|---|
| Datos nominales | Escala nominal | Categórico (Sin orden) | Género, color de ojos | Segmentación de mercado, encuestas |
| Datos ordinales | Escala ordinal | Categorías clasificadas | Nivel educativo, satisfacción | Experiencia del cliente, evaluaciones de desempeño |
| Datos de intervalo | Escala de intervalo | Intervalos iguales, sin cero verdadero | Temperatura (°C), CI | Psicología, Estudios del Clima |
| Datos de proporción | Escala de razón | Intervalos iguales, cero verdadero | Altura, peso, ingresos | Finanzas, Ingeniería, Atención médica |
Caso práctico de análisis en el mundo real:
En 2025, una cadena minorista global utilizó datos ordinales de encuestas de satisfacción del cliente para predecir las tasas de abandono. Al analizar los niveles de satisfacción (desde "muy insatisfecho" hasta "muy satisfecho"), la empresa identificó grupos de clientes en riesgo y redujo el abandono en un 12 % mediante modelos de análisis predictivo.
Otro caso del sector sanitario involucró datos de ratios. Los hospitales realizaron un seguimiento de los tiempos de recuperación de los pacientes y utilizaron estadísticas descriptivas para optimizar los niveles de personal, reduciendo los tiempos de espera en un 18%.
Contexto histórico
El concepto de clasificación de datos se remonta a mediados del siglo XX, cuando el psicólogo Stanley Smith Stevens introdujo los cuatro niveles de medición en 1946. En 2025, su marco sigue siendo fundamental en la ciencia de datos y el análisis estadístico, constituyendo la base del aprendizaje automático moderno y los sistemas de decisión basados en IA.
Los expertos actuales destacan que las raíces históricas de los datos nominales, ordinales, de intervalo y de razón siguen influyendo en las tecnologías emergentes. A medida que los sistemas de IA dependen cada vez más del etiquetado y la categorización de datos, la comprensión precisa de las escalas de medición garantiza un entrenamiento de modelos ético y preciso.
Reflexiones finales
El auge de la ciencia de datos ha hecho que la capacidad de clasificar e interpretar correctamente los datos sea más valiosa que nunca. Comprender los datos nominales y ordinales, así como las escalas de intervalo y de razón, es la base de un análisis de datos preciso y de conclusiones estadísticas fiables.
Para perfeccionar tus habilidades analíticas, explora nuevas técnicas de recopilación de datos, aplica principios rigurosos de medición de datos y mejora continuamente tu capacidad para distinguir entre variables cualitativas y cuantitativas. El futuro del análisis de datos depende de profesionales capaces de transformar datos estadísticos complejos en información útil y práctica.

